(a) $\fcolorbox{white}{yellow}{Matrix and vector.}$ Matrix = A collection of array of numbers. Vector = one array of numbers. Eg. $$ M = \begin{pmatrix} 1 & 0 & -1 \\ 0 & -2 & 3 \\ 1 & 1 & -2 \end{pmatrix}, \mm v = \begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} $$
(b) $\fcolorbox{white}{yellow}{Determinants for 2 by 2 and 3 by 3 matrices}$
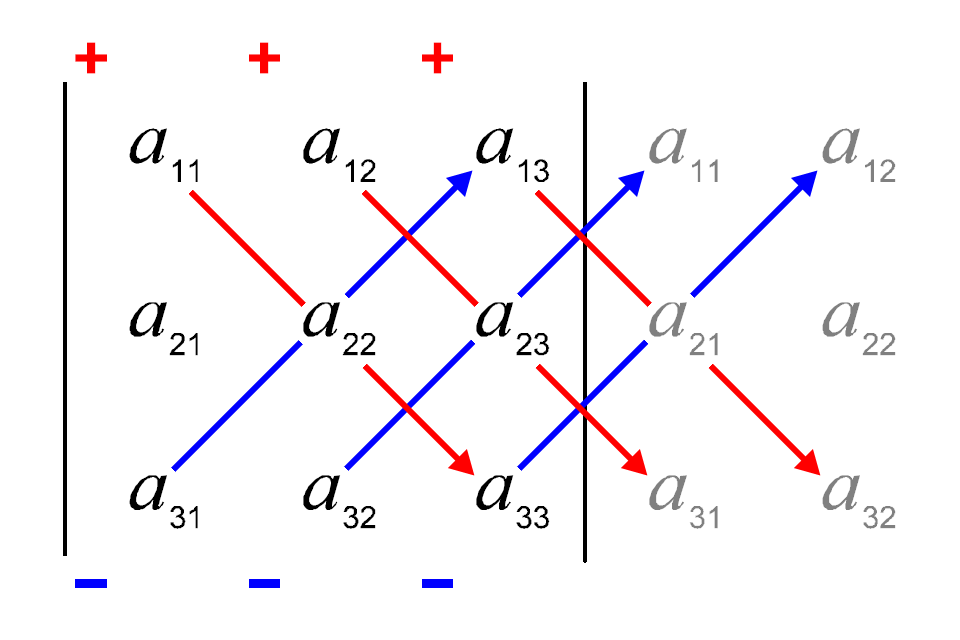
In the case of a 2 × 2 matrix the determinant can be defined as $${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}}$$ Similarly, for a 3 × 3 matrix A, its determinant is $${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}& =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}.\end{aligned}}}$$
(c) $\fcolorbox{white}{yellow}{Cramer's rule:}$ Explicit formulas for small systems. Consider the linear system
$${\displaystyle \left\{{\begin{matrix}a_{1}x+b_{1}y&={\color {red}c_{1}}\\a_{2}x+b_{2}y &={\color {red}c_{2}}\end{matrix}}\right.} $$ which in matrix format is $${\displaystyle {\begin{pmatrix}a_{1}&b_{1}\\a_{2}&b_{2}\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={ \begin{pmatrix}{\color {red}c_{1}}\\{\color {red}c_{2}}\end{pmatrix}}.} $$ Assume the denominator is nonzero. Then, with help of determinants, $x$ and $y$ can be found with Cramer's rule as $$ {\displaystyle {\begin{aligned}x&={\frac {\begin{vmatrix}{\color {red}{c_{1}}}&b_{1}\\ {\color {red}{c_{2}}}&b_{2}\end{vmatrix}}{\begin{vmatrix}a_{1}&b_{1}\\ a_{2}&b_{2}\end{vmatrix}}}={{\color {red}c_{1}}b_{2}-b_{1}{\color {red}c_{2}} \over a_{1}b_{2}-b_{1}a_{2}},\quad y={\frac {\begin{vmatrix}a_{1}&{\color {red}{c_{1}}}\\a_{2}&{\color {red}{c_{2}}}\end{vmatrix}}{\begin{vmatrix}a_{1}&b_{1}\\ a_{2}&b_{2}\end{vmatrix}}}={a_{1}{\color {red}c_{2}}-{\color {red}c_{1}}a_{2} \over a_{1}b_{2}-b_{1}a_{2}}\end{aligned}}.} $$ The rules for 3 × 3 matrices are similar. Given $${\displaystyle \left\{{\begin{matrix}a_{1}x+b_{1}y+c_{1}z &={\color {red}d_{1}}\\a_{2}x+b_{2}y+c_{2}z&={\color {red}d_{2}}\\a_{3}x+b_{3}y+c_{3}z &={\color {red}d_{3}}\end{matrix}}\right.} $$ which in matrix format is $${\displaystyle {\begin{pmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{pmatrix}} {\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}{\color {red}d_{1}}\\{\color {red}d_{2}}\\{\color {red}d_{3}}\end{pmatrix}}.} $$ Then the values of x, y and z can be found as follows: $${\displaystyle x={\frac {\begin{vmatrix}{\color {red}d_{1}}&b_{1}&c_{1}\\{\color {red}d_{2}}&b_{2}&c_{2}\\ {\color {red}d_{3}}&b_{3}&c_{3}\end{vmatrix}}{\begin{vmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{vmatrix}}},\quad y={\frac {\begin{vmatrix}a_{1}&{\color {red}d_{1}}&c_{1}\\a_{2}&{\color {red}d_{2}}&c_{2}\\a_{3}&{\color {red}d_{3}}&c_{3}\end{vmatrix}} {\begin{vmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{vmatrix}}}, \m z={\frac {\begin{vmatrix}a_{1}&b_{1}&{\color {red}d_{1}}\\a_{2}&b_{2}&{\color {red}d_{2}}\\a_{3}&b_{3}&{\color {red}d_{3}}\end{vmatrix}} {\begin{vmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{vmatrix}}}.} $$