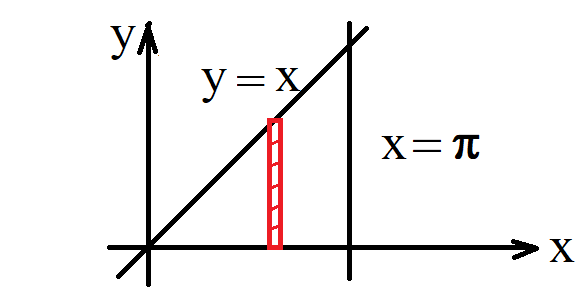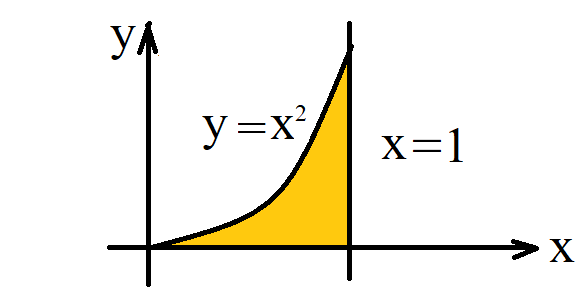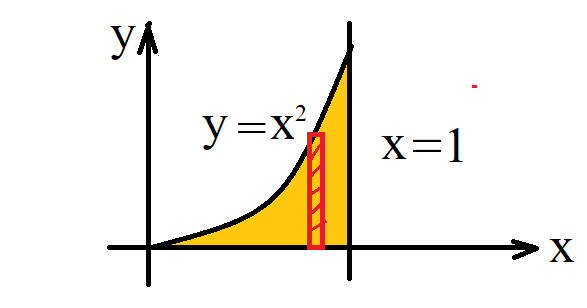Examples of choosing directions.
Ex: $\intd A \frac{\sin x}{x} dxdy$, where $A$ is the area bounded by $y=x$, $x$-axis, and $x=\pi$.

Sol. Try horizontal small rectangles: $\int_{y=0}^\pi \Big(\int_{x=y}^\pi \frac{\sin x}{x} dx \Big) dy$ - does not work.

Now, try vertical small rectangles: $\int_{x=0}^\pi \Big(\int_{y=0}^{x} \frac{\sin x}{x} dy \Big) dx$ $= \int_{x=0}^\pi \Big(\frac{\sin x}{x} y\Big)\Big|_{y=0}^{y=x} dx$ $ = \int_{x=0}^\pi \sin x dx $ $ = - \cos x\Big|_{x=0}^{x=\pi} = -\Big[(-1) - 1\Big] = 2 $

Summary: if one direction does not work, try the other;

The area $A$ is bounded by $x$-axis, $x=1$ and $y=x^2$.

1. The area as a double integral:
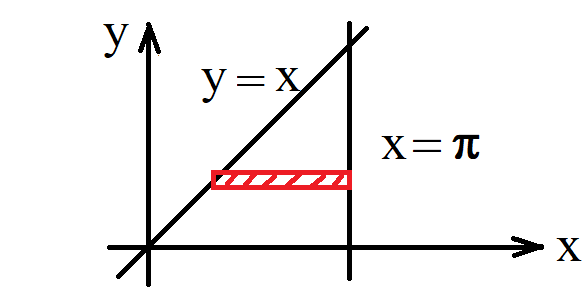
   $A = \intd{A} dxdy, \m dA = dxdy$
   ;

   $A = \intd{A} dxdy$ $=\int_{x=0}^{1}\Big(\int_{y=0}^{x^2} 1 dy\Big)dx $ $= \int_{x=0}^{1} y\Big|_{y=0}^{y=x^2} dx$ $= \int_{x=0}^{1} x^2 dx$ $ = \frac13 x^3\Big|_{x=0}^1 = \frac13$

   
   
   
2. Mass: If the density $\rho(x,y) $ or $\rho(x,y,z)$ is given, then the mass is given by
   2D:
   $M = \intd{A} \rho(x,y) dxdy , \m dM =\rho(x,y) dxdy$
   ;
   
   Suppose in the above example for area under $y=x^2$
   between $x=0$ and $x=1$, $\rho(x,y) = xy$, then
   $M = \intd{A} xy dxdy$
   $=\int_{x=0}^{1}\Big(\int_{y=0}^{x^2} xy dy\Big)dx $
   $= \int_{x=0}^{1} \frac12 xy^2\Big|_{y=0}^{y=x^2} dx$ $= \int_{x=0}^{1} \frac12 x^5 dx$ $ = \frac1{12} x^6\Big|_{x=0}^1 = \frac1{12}$
   
   3D:
   $M = \int\hspace{-0.7em}\intd{V} \rho(x,y,z) dxdydz , \m dM =\rho(x,y,z) dxdydz$
   ;
   
   
   
   
   
   
   
   
3. Arc Length:
   If $y = f(x)$, then
   
   $ ds = \sqrt{ dx^2 + dy^2 } = \sqrt{1+ \Big(\frac{dy}{dx}\Big)^2} dx $
   ;
   
   Suppose in the above example, we like to compute
   the arc length of $y=x^2$ between $x=0$ and $x=1$, then
   $S =\int_{x=0}^{1} \sqrt{1+ \Big(\frac{df}{dx}\Big)^2 } dx $
   $= \int_{x=0}^{1} \sqrt{1+(2x)^2} dx$ $= 4\int_{x=0}^{1} \sqrt{\Big(\frac12\Big)^2 + x^2} dx$
   $ = \frac14\Big\{2\sqrt5 +\ln(2+\sqrt5)\Big\}$
   $ \fcolorbox{white}{yellow}{$\int \sqrt{a^2+u^2} du = \frac{u}2 \sqrt{a^2+u^2} + \frac{a^2}2 \ln( u+\sqrt{a^2+u^2})$} $
   
   
   
   
   
   
4. Center of mass $(\bar x, \bar y, \bar z)$: Writing $\int$ for either $\intd{}$ or $\intd{}\hspace{-0.7em}\int$,
   
   $ \int \bar x dM = \int x dM, \m \int \bar y dM = \int y dM, \m \int \bar z dM = \int z dM, \m dM = \rho(x,y,z)dxdydz $
   ;
   Suppose in the above example, $\rho(x,y)=1$,
   then
   $\intd A \bar x dM = \intd A x dM$, $dM = \rho(x,y) dxdy = dxdy$,
   $\intd A \bar x dM = \bar x \int_{x=0}^{1}\Big(\int_{y=0}^{x^2} dy\Big)dx = \bar x \frac13$
   
   $\intd A x dM = \int_{x=0}^{1}\Big(\int_{y=0}^{x^2} x dy\Big)dx = \int_{x=0}^{1} x^3 dx = \frac1{4}$
   $ \bar x \frac13 = \frac14, \mm \bar x = \frac34$.
   Similarly $ \bar y = \frac3{10}$.